Транзисторы СВЧ
Встроенные модели транзисторов программы PSpice (гл. 4) справедливы на не очень высоких частотах (до 30...100 МГц в зависимости от типа транзистора). Существует несколько способов их модернизации для учета особенностей транзисторов на высоких частотах.
а) Нелинейные макромодели на физическом уровне
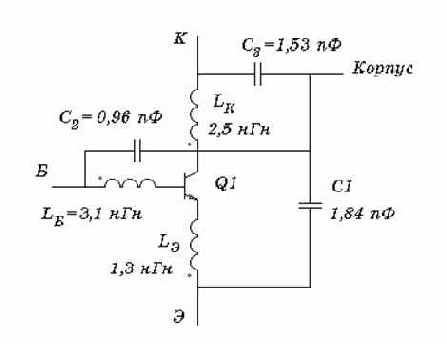
В моделях транзисторов на высоких частотах должны в первую очередь приниматься во внимание индуктивности выводов и паразитные емкости между выводами и корпусом транзистора. Поэтому наиболее естественно создать макромодель высокочастотного транзистора на основе встроенной модели, дополнив ее пассивными LC-цепями. Существует большое количество конфигураций этих цепей, учитывающих конструктивные особенности каждого транзистора. В качестве примера приведем макромодель транзистора 2Т934А (рис. 5.6):
.subckt 2T934A 1 2 3
Q1 4 5 6 Q
L1 2 5 3.1n
L2 1 4 2.5n
L3 6 3 1.3n
C1 2 3 0.96p
C2 1 3 1.53p
.model Q NPN (IS=2nA BF=50 BR=4.6 NF=1.4 NR=1.5 CJE=32p
+ CJC=20p VJE=0.8 VJC=0.8 MJE=0.4 MJC=0.45 TF=0.18n
+ TR=4.5n VAF=80 RB=1.4 RC=1.3)
.ends
|
Рис. 5.6. Нелинейная макромодель транзистора 2Т934А |
Подобные модели позволяют рассчитывать как режим по постоянному току, так и динамические характеристики устройств.
б) Малосигнальные макромодели на физическом уровне
В высокочастотной транзисторной электронике усилительные свойства транзисторных каскадов оценивают на основе сложных малосигнальных схем замещения транзисторов, пример которых приведен на рис. 5.7, а. Текстовое описание модели биполярного транзистора КТ642 для тока коллектора 5 мА в файле KT642.mod приведено ниже:
.subckt KT642 5 11 10
*KT642A-2, Ie=5 mA, Ft=4 G
GK 6 3 LAPLACE {I(VE)} {1/(1+S/25E9)}
RB 2 6 4.0
CP 2 3 0.5p
RK 3 4 1.2
CA 6 3 0.5p
RDB 1 2 0.1
LK 4 5 0.1n
CE 7 6 4P
LB 1 11 0.1n
RDE 8 7 0.5
LE 9 8 0.1n
RE 7 6 5.0
VE 10 9 0V
.ENDS
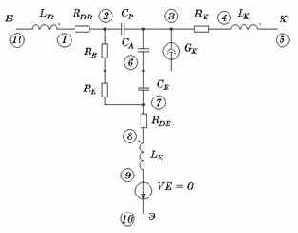 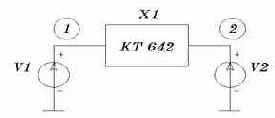 Рис. 5.7. Линейная высокочастотная макромодель транзистора КТ642 (а) и схема измерения его Y-параметров (б) |

GK 6 3 LAPLACE {I(VE)} {1/(1+S/25e9)}
В моделях полевых транзисторов используются операторы запаздывания, например
GC 10 7 LAPLACE {V(3)} {18e-3*EXP(-1.2e-10*S)}
Примечание. Идентификация параметров малосигнальных схем замещения транзисторов производится на основе расчета их Y–параметров в схеме, показанной на рис. 5.7, б. В текстовом виде задание на моделирование имеет вид:
Y-parameters calculation
.AC LIN 101 10MEG 1G
.PROBE
.param A=1
.step param A list 1 0
V1 1 0 AC {A}
V2 2 0 AC {1-A}
X1 1 2 KT642
.inc KT642.mod
.END
Здесь в одном задании проводятся два опыта при коротком замыкании на выходе (параметр А=1) и коротком замыкании на входе (А=0). Для построения с помощью программы Probe графиков мнимых и действительных частей Y–параметров и инвариантного коэффициента устойчивости KMS рекомендуется в файл msim.prb включить макрокоманды
RY11( )=-(IR(V1)@1*VR(1)@1+II(V1)@1*VI(1)@1)/M1
IY11( )=-(II(V1)@1*VR(1)@1-IR(V1)@1*VI(1)@1)/M1
IY21( )=-(II(V2)@1*VR(1)@1-IR(V2)@1*VI(1)@1)/M1
RY21( )=-(IR(V2)@1*VR(1)@1+II(V2)@1*VI(1)@1)/M1
RY12( )=-(IR(V1)@2*VR(2)@2+II(V1)@2*VI(2)@2)/M2
IY12( )=-(II(V1)@2*VR(2)@2-IR(V1)@2*VI(2)@2)/M2
RY22( )=-(IR(V2)@2*VR(2)@2+II(V2)@2*VI(2)@2)/M2
IY22( )=-(IR(V2)@2*VR(2)@2+II(V2)@2*VI(2)@2)/M2
M1( )=M(V(1)@1)*M(V(1)@1)
M2( )=M(V(2)@2)*M(V(2)@2)
KMS( ) = 10*log10(I(V2)@1/V(1)@1/I(V1)@2*V(2)@2)
Для построения, например, графика частотной зависимости мнимой составляющей Y11 следует выбрать команду Trace/Add
и указать имя макрокоманды IY11 (без параметров).
в) Формальные малосигнальные макромодели
Второй способ построения высокочастотных моделей транзисторов основан на применении их малосигнальных схем замещения.
В таком случае сначала с помощью типовых моделей транзисторов рассчитывается режим цепи по постоянному току и для этого режима измеряются или рассчитываются Y-или S-параметры транзисторов в заданном диапазоне частот. Рассмотрим эти схемы замещения для программы PSpice подробнее.
Макромодель на основе Y-параметров. Напомним уравнение линейного 4-полюсника (рис. 5.8) в системе Y-параметров

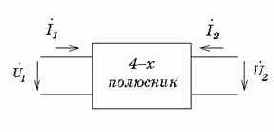 Рис. 5.8. Линейный 4-полюсник |
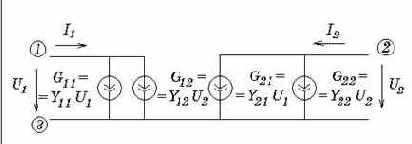 Рис. 5.9. Макромодель транзистора на основе Y-параметров |
Приведем пример формальной макромодели транзистора КТ315В на основе Y-параметров, измеренных на частотах 5, 10 и 30 МГц для тока коллектора Iк=5 мА:
.subckt KT315V 2 1 3
G11 1 3 FREQ {V(1,3)}=
+ ( 5e6, -50.3, 31.6) (10e6, -48.0, 36.9) (30e6, -44.3, 41.0)
G12 1 3 FREQ {V(2,3)}=
+ ( 5e6, -78.4, 181.9) (10e6, -72.7, 184.5) (30e6, -63.1, 183.7)
G21 2 3 FREQ {V(1,3)}=
+ ( 5e6, -18.7, -20.8) (10e6, -20.0, -31.9) (30e6, -25.5, -44.2)
G22 2 3 FREQ {V(2,3)}=
+ ( 5e6, -67.4, 63.4) (10e6, -63.3, 56.3) (30e6, -59.4, 54.1)
.ends
Напомним, что при табличном задании управляемых источников в частотной области для каждого значения частоты указывается модуль передаточной функции в децибелах и ее фаза в градусах.
Макромодель на основе S-параметров. В диапазоне СВЧ большее распространение имеют линейные макромодели транзисторов на основе S-параметров, которые в этом диапазоне частот проще измерять, чем Y-параметры. Напомним, что для 4-полюсника на рис. 5.8 справедливо следующее уравнение в терминах S-параметров [27, 44]:

Здесь

– падающие и отраженные волны мощности, Z

волновое сопротивление тракта, в котором измерены S-параметры транзистора.
Из этих соотношений вытекают уравнения для входного и выходного напряжений, в которые входят управляемые источники напряжения:

где

На основе этой системы уравнений составляется линеаризованная схема замещения СВЧ транзистора (рис. 5.10). В качестве примера приведем описание макромодели арсенид– галлиевого полевого транзистора 3П343 в диапазоне частот 4...12 ГГц при напряжении затвора 2 В и токе стока 10 мА:
.subckt 3P343 2 1 3
RZ1 1 11 50
RZ2 2 21 50
E11 11 12 FREQ {V(1,3)+V(1,11)} =
+ (4e9, -0.35, -28.3) (5e9, -0.54, -33.2) (6e9, -0.58, -35.9)
+ (7e9, -1.21, -41.9) (8e9, -1.01, -67.1) (9e9, -2.85, -56.9)
+ (10e9, -4.29, -32.8) (11e9, -1.94, -56.9) (12e9, -0.63, -65.2)
E12 12 3 FREQ {V(2,3)+V(2,21)}=
+ (4e9, -32.5, 77.0) (5e9, -29.5, 62.0) (6e9, -29.2, 72.4)
+ (7e9, -27.3, 65.0) (8e9, -23.5, 15.0) (9e9, -29.0, 66.1)
+ (10e9, -23.4, 36.6) (11e9, -25.4, 61.7) (12e9, -22.1, 40.4)
E21 21 22 FREQ {V(1,3)+V(1,11)}=
+ (4e9, 0.82, 149.8) (5e9, 2.30, 131.1) (6e9, 0.74, 134.3)
+ (7e9, 1.26, 129.0) (8e9, 0.43, 105.5) (9e9, 0.11, 123.2)
+ (10e9, 3.92, 87.5) (11e9, 2.40, 110.1) (12e9, 4.10, 85.0)
E22 22 3 FREQ {V(2,3)+V(2,21)}=
+ (4e9, -2.16, -26.4) (5e9, -1.21, -49.1) (6e9, -2.27, -45.1)
+ (7e9, -2.21, -34.4) (8e9, -2.62, -54.5) (9e9, -2.73, -52.7)
+ (10e9, -3.74, -17.2) (11e9, -3.48, -65.1) (12e9, -4.44, -62.4)
.ends
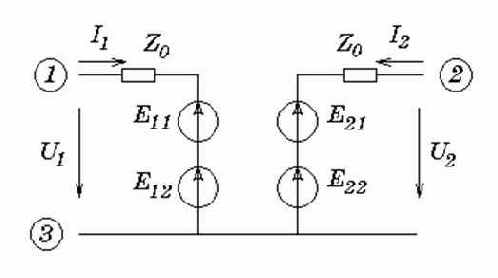 Рис. 5.10. Макромодель транзистора на основе S-параметров |