Следящая система

Программа PSpice разработана для моделирования нелинейных электрических цепей, заданных принципиальными электрическими схемами. Но это не препятствует моделированию систем автоматики, заданных функциональными схемами. Необходимо лишь каждому элементу функциональной схемы поставить в соответствие схему замещения из компонентов, допустимых в PSpice. Наиболее удобно это делать с помощью линейных и нелинейных управляемых источников (см. 3.2.4, 3.2.5).

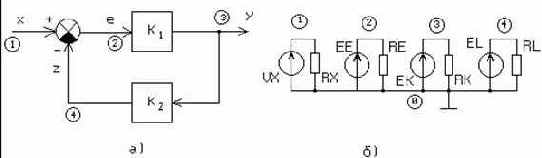
Проиллюстрируем эту методику на примере следящей системы с отрицательной обратной связью, показанной на рис. 3.24, а, где передаточная функция

.  Моделирование проведем двумя способами.

1. Сначала с помощью старой версии PSpice все три блока функциональной схемы – сумматор, усилитель с коэффициентом передачи K

и фильтр с передаточной функцией G(s)

– реализуем с помощью линейных источников напряжения EE, EK, EZ, управляемых напряжениями, как показано на рис. 3.24, б. Источник сигнала имитируется независимым источником напряжения

VX. Параллельно каждому источнику включены сопротивления RX, RE, RK, RZ, чтобы в схеме замещения не было разомкнутых контуров (это требование PSpice, связанное с ошибками в программе контроля топологии). Потенциалы узлов в схеме на рис. 3.24, б соответствуют значениям переменных в одноименных точках функциональной схемы на рис. 3.24, а. Приведем задание на расчет частотных характеристик этой системы:

СЛЕДЯЩАЯ СИСТЕМА С ТРЕХЗВЕННОЙ RC-ЦЕПЬЮ

.PARAM  K=1  A=20  TAU=0.1

VX  1  0  AC=1

RX  1  0  1

*EE  0  2  VALUE={V(1)-V(4)}          ; ОС замкнута

EE  0  2  VALUE={V(1)}                    ; ОС разомкнута

RE  2  0  1

EK  0  3  VALUE={K*V(2)}

RK  3  0  1

EL  4  0  LAPLACE {V(3)} {A/((1+TAU*s)*(1+TAU*s)*(1+TAU*s))}

RL  4  0  1

.AC  LIN  500  0.01 10

.WATCH  AC  V(2)  V(3)  V(4)

.PROBE

.END

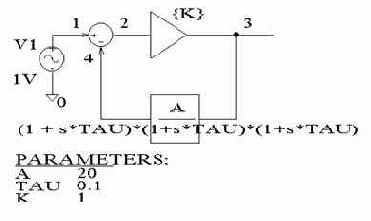
Рис. 3.24.  Функциональная схема следящей системы (а), ее модель для старой версии PSpice (б) и графическое изображение в Schematics (в)

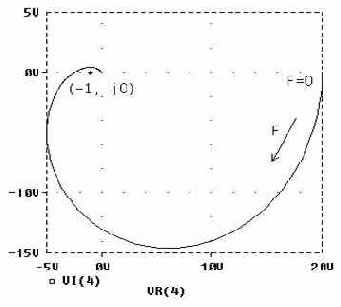
Здесь предусмотрено два варианта сумматора EE

– для моделирования следящей системы с замкнутой и разомкнутой обратной связью. Последнее используется для исследования устойчивости следящей системы с помощью критерия Найквиста. Годограф коэффициента передачи разомкнутой системы для иллюстрации показан на рис. 3.25: точка на комплексной плоскости с координатами (–1, j0) годографом не охватывается, поэтому рассматриваемая система устойчива.

Рис. 3.25. Годограф коэффициента передачи разомкнутой следящей системы

2. В Design Center 6.2 больше не нужно подсоединять фиктивные резисторы к  управляющим входам функциональных источников – в результате функциональная схема следящей системы (рис. 3.24, а), нарисованная в Sсhematics, имеет естественный вид (рис. 3.24, в). В то же время текстовое задание на моделирование, помещающееся теперь в трех файлах с расширениями .cir, .net и .als, изменилось незначительно:

Файл control.cir

* C:\MSIM62J\EXAMPLES\CONTROL.SCH

* Schematics Version 6.2j - December 1995

* Fri Feb 02 16:17:26 1996

.PARAM    A=20   TAU=0.1   K=1

** Analysis setup **

.ac   LIN   501   0.01   10

* From [SCHEMATICS NETLIST] section of msim.ini:

.lib   C:\MSIM62J\LIB\MY.LIB

.lib   nom.lib

.INC  "CONTROL.net"

.INC  "CONTROL.als"

.probe

.END

Файл control.net

* Schematics Netlist *

V_V1         1    0   DC   0V   AC   1V

E_DIFF1   2   0   VALUE {V(1,4)}

E_GAIN1  3   0   VALUE {{K} * V(2)}

E_LAPLACE1    4   0   LAPLACE {V(3)} {(A)/((1 + s*TAU)*

+  (1+s*TAU)*(1+s*TAU))}

Файл control.als

* Schematics Aliases *

.ALIASES

V_V1                V1(+=1 -=0 )

E_DIFF1          DIFF1(OUT=2 IN2=1 IN1=4 )

E_GAIN1          GAIN1(OUT=3 IN=2 )

E_LAPLACE1          LAPLACE1(OUT=4 IN=3 )

_    _(1=1)

_    _(2=2)

_    _(4=4)

_    _(3=3)

.ENDALIASES

В заключение отметим, что разнообразным применениям программы PSpice посвящены работы [35, 49, 55]. В статье [36] обсуждаются специфические вопросы исследования переходных процессов в коммутируемых цепях.Практические советы по моделированию регулярно помещаются в журнале “The Design Center Source”, выпускаемом корпорацией MicroSim.


Содержание раздела

---

---