Пассивные компоненты
Резисторы описываются предложением
Rxxx <+узел> <–узел> [ имя модели ] <значение> [ TC=<TC1>[,<TC2> ] ]
Здесь xxx – произвольная алфавитно-цифровая последовательность общей длиной не более 7 символов, которая пишется слитно с символом R и вместе с ним образует имя компонента. Например:
R1 15 0 2K
RGEN 1 2 2.4E4
R12 3 0 RTEMP 5K
.MODEL RTEMP RES (R=3 DEV=5% TC1=0.01)
Параметры, описывающие модель резистора, приведены в табл. 3.7.
Таблица 3.7
| Обозначение | Параметр | Размерность | Значение по умолчанию | ||||
| R | Масштабный множитель сопротивления | 1 | |||||
| TC1 | Линейный температурный коэффициент сопротивления |   | 0 | ||||
| TC2 | Квадратичный температурный коэффициент сопротивления |   | 0 | ||||
| TCE | Экспоненциальный температурный коэффициент сопротивления | %/ | 0 | ||||
| T_MEASURED | Температура измерений |  | |||||
| T_ABS | Абсолютная температура |  | |||||
| T_REL_GLOBAL | Относительная температура |  | |||||
| T_REL_LOCAL | Разность между температурой устройства и модели-прототипа |  |
Если в описании резистора <имя модели> опущено, то его сопротивление равно параметру <сопротивление> в омах. Если <имя модели> указано и в директиве .MODEL отсутствует параметр TCE, то сопротивление резистора определяется выражением
<значение>


если же параметр TCE указан, то сопротивление равно
<значение>



Здесь T – текущее значение температуры (указывается по директиве .TEMP); Tnom=27

Параметр <значение> может быть как положительным, так и отрицательным, но не равным нулю.
Спектральная плотность теплового тока резистора рассчитывается по формуле Найквиста S

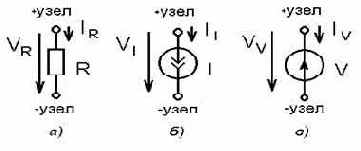 - источник тока; в - источник напряжения |
Конденсатор описывается предложением
Cxxx <+узел> <–узел> [имя модели] <значение>
+ [IC=<начальное значение напряжения>]
Например:
C1 15 0 56PF
C2 3 9 0.5PF IC=1.5V
C3 4 6 CMOD 10U
.MODEL CMOD CAP (C=2.5 TC1=0.01 VC1=0.2)
Параметры модели конденсатора приведены в табл. 3.8.
Таблица 3.8
|
Обозначение |
Параметр |
Размерность |
Значение по умолчанию |
|
С |
Масштабный множитель емкости |
|
1 |
|
VC1 |
Линейный коэффициент напряжения |
В |
|
|
VC2 |
Квадратичный коэффициент напряжения |
В |
|
|
TC1 |
Линейный температурный коэффициент емкости |
  |
0 |
|
TC2 |
Квадратичный температурный коэффициент емкости |
  |
0 |
|
T_MEASURED |
Температура измерений |
 |
|
|
T_ABS |
Абсолютная температура |
 |
|
|
T_REL_GLOBAL |
Относительная температура |
 |
|
|
T_REL_LOCAL |
Разность между температурой устройства и модели-прототипа |
 |
<значение>





Здесь V – напряжение на конденсаторе при расчете переходных процессов (режим TRAN). При расчете частотных характеристик (режим AC) емкость считается постоянной величиной, определяемой в рабочей точке по постоянному току.
После ключевого слова IC указывается значение напряжения на конденсаторе при расчете режима по постоянному току, которое при расчете переходных процессов служит начальным значением этого напряжения.
Индуктивность описывается пpедложением
Lxxx <+узел> <–узел> [имя модели] <значение>
+ [IC = <начальное значение тока>]
Например:
L1 15 0 20MH
L2 1 2 0.2E-6
L3 4 6 2VH IC=2
LOAD 5 12 LMOD 0.03
.MODEL LMOD IND (L=2 DEV=20% IL1=0.1)
Параметры модели индуктивности приведены в табл. 3.9.
Таблица 3.9
|
Обозначение |
Параметр |
Размерность |
Значение по умолчанию |
|
L |
Масштабный множитель индуктивности |
1 |
|
|
IC1 |
Линейный коэффициент тока |
А |
|
|
IC2 |
Квадратичный коэффициент тока |
А |
|
|
TC1 |
Линейный температурный коэффициент индуктивности |
  |
0 |
|
TC2 |
Квадратичный температурный коэффициент индуктивности |
  |
0 |
|
T_MEASURED |
Температура измерений |
 |
|
|
T_ABS |
Абсолютная температура |
 |
|
|
T_REL_GLOBAL |
Относительная температура |
 |
|
|
T_REL_LOCAL |
Разность между температурой устройства и модели-прототипа |
 |
<значение>





Здесь I – ток через катушку индуктивности при расчете переходных процессов (режим TRAN). При расчете частотных характеристик (режим AC) индуктивность считается постоянной величиной, определяемой в рабочей точке по постоянному току.
После ключевого слова IC указывается значение тока через катушку индуктивностей при расчете режима по постоянному току, которое при расчете переходных процессов служит начальным значением этого тока.
Взаимная индуктивность
описывается предложением
Kxxx Lyyy Lzzz ... <коэффициент связи>
Первое предложение описывает связанные индуктивности без сердечника, второе – с ферромагнитным сердечником, третье – связанные линии передачи.
Порядок перечисления имен индуктивностей Lyyy, Lzzz ... безразличен, знак взаимной индуктивности определяется порядком перечисления узлов в описании каждой индуктивности.
Параметром взаимной индуктивности является <коэффициент связи>. Если в трансформаторе имеется несколько обмоток, то можно либо определить взаимные индуктивности для каждой попарной комбинации обмоток в отдельных предложениях, либо в одном предложении указать список всех индуктивностей, имеющих одинаковый коэффициент связи. Например, трехобмоточный высокочастотный трансформатор (рис. 3.2) описывается следующим образом:
I1 1 0 AC 1MA
L1 1 0 10UH
L2 2 3 10UH
L3 3 4 10UH
K12 L1 L2 L3 0.8
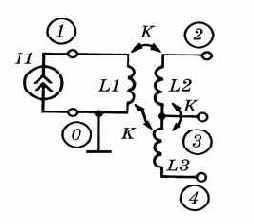 |
Коэффициент связи двух обмоток определяется выражением
коэффициент связи =

где L





Магнитный сердечник трансформатора описывается предложением
Kxxx Lyyy Lzzz ... <коэффициент связи> <имя модели>
+ [<масштабный коэффициент>]
На одном сердечнике помещается одна или несколько обмоток с именами Lyyy, Lzzz ... . Все обмотки имеют одинаковый <коэффициент связи>. При описании каждой обмотки Lyyy ..., упомянутой в составе сердечника, изменяется смысл параметра <значение> – теперь он определяет не индуктивность, а число витков обмотки сердечника. Например, трансформатор с пермаллоевым сердечником МП60 (рис. 3.3) описывается предложениями:
L1 15 10 50; 50 витков
L2 10 0 150; 150 витков
K2 L1 L2 0.99 Ti125V
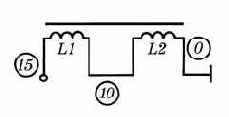 |
+ A=4.05E3 K=166 C=0.05 AREA=0.064 PATH=2.25)
Параметр <масштабный коэффициент> изменяет площадь поперечного сечения магнитопровода (по умолчанию равен единице).
Она равна произведению этого коэффициента на параметр модели сердечника AREA.
Параметры модели магнитного сердечника приведены в разд. 4.6. График кривой намагниченности сердечника выводится на экран с помощью директивы .PROBE (разд. 3.3.5); с помощью директив .PRINT и .PLOT эти данные не выводятся.
Линия передачи описывается двояко. Линия передачи без потерь
описывается предложением
Txxx <+узел порта A> <–узел порта A> <+узел порта B> <–узел порта B>
+ [имя модели] ZO=<значение> [TD=<значение>]
+ [F = <значение> [NL = <значение>]]
+ IC=<напряжение на входе А> <ток входа A>
+ <напряжение на входе B> <ток входа B>
Здесь ZO – волновое сопротивление линии (Ом), TD – задержка сигнала в линии (с), NL – электрическая длина линии на частоте F (NL=l/l, где l – геометрическая длина линии, l – длина волны в линии, по умолчанию NL=0,25). При описании линии передачи задается параметр TD либо F и NL. Например,
T1 1 2 3 4 ZO = 50
T2 1 2 3 4 ZO = 75 TD = 115NS
T3 1 2 3 4 ZO = 75 F = 4.5MEG
T4 1 2 3 4 ZO = 75 F = 4.5MEG NL = 0.5
С помощью ключевого слова IC задаются начальные значения напряжений и токов на выводах линии передачи.
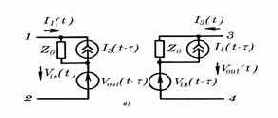 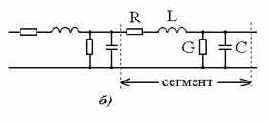 Рис. 3.4. Модель линии передачи без потерь (а) и с учетом потерь (б) |
Линия передач с потерями
описывается предложением
Txxx <+узел порта A> <–узел порта A> <+узел порта B> <–узел порта B>
+ [<имя модели> [электрическая длина ] ] LEN=<значение>
+ R=<значение> L=<значение> G=<значение> C=<значение>
Здесь LEN – длина линии (м); R, L, G, C – погонное сопротивление линии (Ом/м), погонная индуктивность (Гн/м), проводимость (См/м), емкость (Ф/м).
В принципе длину линии можно указывать в любых единицах, например в километрах, но тогда нужно соответствующим образом пересчитать значения погонных параметров R, L, G и C.
По этим данным аналитически рассчитывается комплексный коэффициент передачи линии. Анализ переходных процессов производится с помощью интеграла свертки с импульсной характеристикой линии, которая вычисляется как преобразование Фурье коэффициента передачи.
Модель линии передачи описывается предложением (начиная с версии Design Center 6.1):
.MODEL <имя модели> TRN (параметры модели)
Модель линии передачи характеризуется параметрами, указанными в табл. 3.10.
Таблица 3.10
|
Обозначение |
Параметр |
Размерность |
Значение по умолчанию |
|
Идеальная линия без потерь |
|||
|
ZO |
Волновое сопротивление |
Ом |
|
|
TD |
Время задержки сигнала |
с |
|
|
F |
Частота для расчета NL |
Гц |
|
|
NL |
Электрическая длина на частоте F |
0,25 |
|
|
IC |
Начальные значения напряжений и токов |
||
|
Линия с потерями |
|||
|
R |
Погонное сопротивление |
Ом/м |
|
|
L |
Погонная индуктивность |
Гн/м |
|
|
G |
Погонная проводимость |
См/м |
|
|
C |
Погонная емкость |
Ф/м |
|
|
LEN |
Электрическая длина |
м |
2. Принятая в программе PSpice 6.2 модель линии передачи с потерями требует больших затрат времени и не обеспечивает достаточную точность расчетов. Поэтому иногда приходится самостоятельно составлять цепочечные схемы замещения линий передачи с потерями (рис. 3.4, б).
3. В представленных моделях, к сожалению, не учитываются частотные зависимости погонных параметров R, L и G, существенные при моделировании реальных протяженных линий передачи. Это можно сделать, начиная с версии PSpice 5.3, задавая преобразования Лапласа параметров R(s) и G(s) – имитация частотной зависимости поверхностного эффекта и потерь в диэлектрике.
Связанные линии передачи описываются предложением
Kxxx T<имя 1-й линии передачи> T<имя 2-й линии передачи>
+ Cm=<взаимная емкость> Lm=<взаимная индуктивность>
Здесь Cm и Lm – взаимные емкости и индуктивности связанных линий [75, 80].
