Независимые источники сигналов
Стандартные сигналы
Независимые источники напряжения (V) и тока (I) стандартного вида описываются предложениями
Vxxx <+узел> <–узел> [[ DC ] <значение>] [AC <модуль> [<фаза>]]
+ [ STIMULUS=<имя сигнала> ] [ спецификация сигнала ]
Ixxx <+узел> <–узел> [[DC] <значение>] [AC <модуль> [<фаза>]]
+ [STIMULUS=<имя сигнала>] [спецификация сигнала ]
После ключевого слова STIMULUS указывается имя сигнала, созданного с помощью программы StmEd. При анализе переходных процессов можно использовать один из стандартных сигналов с помощью конструкции <спецификация сигнала>, имеющий вид
PULSE <параметры> – импульсный сигнал;
SIN <параметры> – синусоидальный сигнал;
EXP <параметры> – сигнал экспоненциальной формы;
PWL <параметры> – кусочно-линейный сигнал;
SFFM <параметры> – гармонический сигнал с синусоидальной частотной модуляцией.
Источники могут использоваться во всех видах анализа. По умолчанию все параметры принимают нулевые значения. Параметр DC определяет постоянную составляющую источника напряжения или тока. Для режима AC задаются модуль и фаза (в градусах) источника гармонического сигнала. Приведем примеры:
IBIAS 13 0 2.3MA
VAC 2 3 AC .001
VACPHS 2 3 AC .001 90
I3 26 77 DC 0.002 AC 1 SIN(.002 0.05 1.5MEG)
При анализе переходных процессов задаются следующие виды временных зависимостей.
Экспоненциальная функция
задается списком параметров
EXP (

и описывается выражением

График этой функции приведен на рис. 3.5, а назначение ее параметров объясняется в табл. 3.12.
Таблица 3.12
| Обозначение | Параметр | Размерность | Значение по умолчанию | ||||
y | Начальное значение | B или A | |||||
y | Максимальное значение | B или A | |||||
t | Начало переднего фронта | с | 0 | ||||
t | Постоянная времени переднего фронта | c | TSTEP * | ||||
t | Начало заднего фронта | с | t | ||||
t | Постоянная времени заднего фронта | с | TSTEP |
* TSTEP – шаг по времени вывода на печать результатов расчетов переходных процессов (задается в директиве .TRAN).
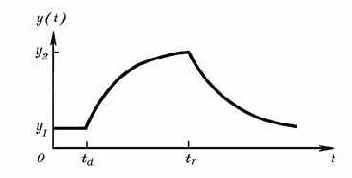 |
V1 3 4 EXP ( 0.02 2NS 20NS 40NS 20NS)
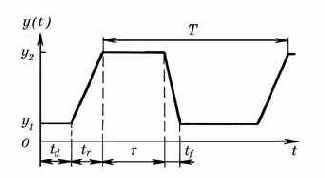
Импульсная функция (рис. 3.6) задается списком параметров
PULSE (

Смысл ее параметров объясняется в табл. 3.13.
Таблица 3.13
|
Обозначение |
Параметр |
Размерность |
Значение по умолчанию |
y |
Начальное значение |
B или A |
|
y |
Максимальное значение |
B или A |
|
t |
Начало переднего фронта |
с |
0 |
t |
Длительность переднего фронта |
с |
TSTEP* |
t |
Длительность заднего фронта |
с |
TSTEP |
 |
Длительность плоской части импульса |
с |
TSTOP** |
|
T |
Период повторения |
с |
TSTOP |
** TSTOP – конечное время анализа переходного процесса (параметры TSTEP и TSTOP задаются в директиве .TRAN).
 |
задается списком параметров
PWL [ TIME_SCALE_FACTOR=<значение> ]
+ [ VALUE_SCALE_FACTOR=<значение> ]
+ (точки_отсчета)*
В секции (точки_отсчета) помещаются следующие данные:

FILE <имя файла> – чтение координат точек из файла;
REPEAT FOR <n> (точки_отсчета)* ENDREPEAT – повторение n раз;
REPEAT FOREVER (точки_отсчета)* ENDREPEAT – бесконечное повторение.
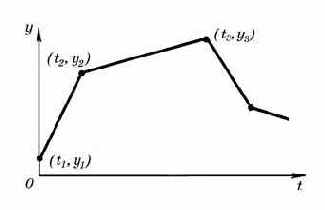
PWL представляет собой кусочно-линейную функцию y(t).
Соседние точки соединяются прямыми линиями (рис. 3.7). Максимальное количество точек для IBM PC составляет 3995.
 |
Приведем примеры.
1) Ступенчатое напряжение – 10 периодов по 1 мкс:
.PARAM N=1
.STEP PARAM N 1,5,1
V1 1 0 PWL
+ TIME_SCALE_FACTOR=1e-6; Время задано в миллисекундах
+ REPEAT FOR 10
+ (.25, 0) (.26, {N}) (.99, {N}) (1,0)
+ ENDREPEAT
2) Считывание сигнала из файла :
V2 1 0 PWL FILE triangle.in
В текстовом файле файле triangle. in содержатся значения отсчетов, например
(1ms, 1) (2ms, 0) (3ms, 1) (4ms, 0)
Синусоидальная функция
задается списком параметров
SIN (

и описывается выражением

Eе параметры описаны в табл. 3.14.
Таблица 3.14
|
Обозначение |
Параметр |
Размерность |
Значение по умолчанию |
y |
Постоянная составляющая |
B или A |
|
y |
Амплитуда |
B или A |
|
|
f |
Частота |
Гц |
1/TSTOP |
t |
Задержка |
с |
0 |
d |
Коэффициент затухания |
1/с |
0 |
|
j |
Фаза |
град. |
0 |


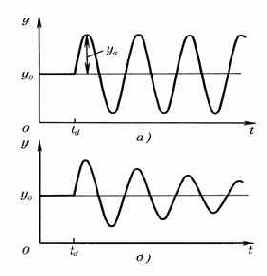 Рис. 3.8. Незатухающая (а) и затухающая (б) синусоидальные функции |
задается списком параметров
SFFM (

и описывается выражением

Eе параметры приведены в табл. 3.15.
Таблица 3.15
|
Обозначение |
Параметр |
Размерность |
Значение по умолчанию |
y |
Постоянная составляющая |
B или A |
- |
y |
Амплитуда |
B или A |
- |
f |
Частота несущей |
Гц |
1/TSTOP |
|
m |
Индекс частотной модуляции |
- |
0 |
f |
Частота модуляции |
Гц |
1/TSTOP |
В связи с тем что программа PSpice имеет довольно бедный набор встроенных источников стандартных сигналов, интересно обсудить возможность генерации сигналов произвольной формы y(t).
В этих целях можно использовать генератор цифровых сигналов (разд. 6.3), логические состояния которого при подключении к аналоговой части схемы автоматически преобразуются в импульсное электрическое напряжение, которое может служить источником сигнала. При необходимости импульсное напряжение сглаживается аналоговым фильтром.
Форма цифрового сигнала задается двояко:
1) путем задания дискретных отсчетов

2) путем предварительной записи отсчетов

Второй способ предпочтительнее при формировании длинных отрезков реализаций сигналов сложной формы, в частности случайных сигналов. Отметим, что формируемые таким образом импульсные сигналы имеют постоянное значение на интервале между дискретными отсчетами:




В Design Center 6.1 появилась возможность считывать координаты аналогового кусочно-линейного сигнала PWL из файла [21] (см. выше).
3.2.4. Зависимые источники сигналов
Зависимые источники напряжения и тока могут быть как линейными, так и нелинейными. Существует четыре их разновидности:
v = е(v) – источник напряжения, управляемый напряжением (ИНУН);
i = f(i) – источник тока, управляемый током (ИТУТ);
i = g(v) – источник тока, управляемый напряжением (ИТУН);
v = h(i) – источник напряжения, управляемый током (ИНУТ).
Линейные управляемые источники
описываются зависимостями v=e·v, i=f·i, i=g·v, v=h·i, где e, f, g и h – коэффициенты передачи.
В описании нелинейных зависимых источников y=y(x




Здесь x



При одномерном управлении (n=1) допускается следующая форма полинома y(x):

При n=2 полином приобретает вид

Рассмотрим подробно все четыре типа зависимых источников.
Источник напряжения, управляемый напряжением
(ИНУН), задается предложениями:
линейный источник
Exxx <+узел> <–узел> <+управляющий узел>
+ <–управляющий узел> <коэффициент передачи>
нелинейный источник
Exxx <+узел> <–узел>
+ POLY(<n>) <<+управляющий узел> <–управляющий узел>>*
+ <коэффициент полинома>*
Например, линейный источник ELIN=

ELIN 1 2 10 11 2.5
Нелинейный источник ENONLIN=

ENONLIN 50 51 POLY(2) (3,0) (4,6) 0.0 13.6 0.2 0.005
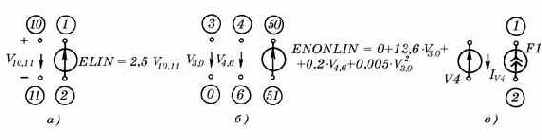 |
(ИТУТ), задается следующим образом:
линейный источник
Fxxx <+узел><–узел> <имя управляющего источника напряжения>
+ <коэффициент передачи>
нелинейный источник
Fxxx <+узел> <–узел>
+ POLY(<n>) <имя управляющего источника напряжения>*
+ <коэффициент полинома>*
Управляющим током служит ток независимого источника напряжения. Например, линейный источник тока

F1 2 1 V4 7.5
Нелинейный источник тока

FNONLIN 10 11 POLY(2) VC1 VC2 0.01 13.6 0.2 0.005 0.001
Источник тока, управляемый напряжением
(ИТУН), задается предложениями:
линейный источник
Gxxx <+узел> <–узел> <+управляющий узел> <–управляющий узел>
+ <коэффициент передачи>
нелинейный источник
G <+узел> <–узел>
+ POLY(<n>) <<+управляющий узел> <–управляющий узел>>*
+ <коэффициент полинома>*
Источник напряжения, управляемый током
(ИНУТ), задается следующим образом:
линейный источник
Hxxx <+узел> <–узел> <имя управляющего источника напряжения>
+<коэффициент передачи>
нелинейный источник
Hxxx <+узел> <–узел>
+ POLY(<n>) <имя управляющего источника напряжения>*
+ <коэффициент полинома>*
Замечание. В связи с тем что в описаниях линейных управляемых источников не допускается использование параметров и функций, в этих целях можно воспользоваться зависимыми источниками с нелинейными передаточными функциями (см. 3.2.5).
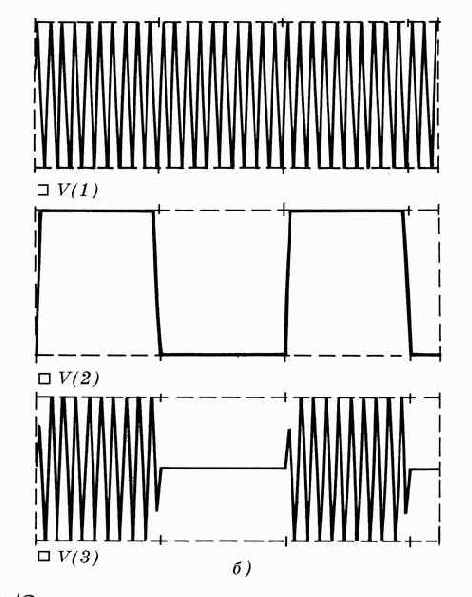
Одно из применений нелинейных зависимых источников – генерация амплитудно-модулированных сигналов. В качестве примера на рис. 3.10, а
показана схема создания источника радиоимпульсов, а на рис. 3.10, б – эпюры напряжений, полученные в результате выполнения следующего задания на моделирование:
RADIOSIGNAL
VSIN 1 0 SIN(0 1 100)
VPULSE 2 0 PULSE(0 1 0 0.25 0.25 0.5 1)
GSIGNAL 0 3 POLY(2) (1,0) (2,0) 0 0 0 0 1
R1 1 0 1MEG
R2 2 0 1MEG
R3 3 0 1MEG
.TRAN 0.01 1.6
.PROBE V(1) V(2) V(3)
.END
 |
Наличие зависимых источников позволяет моделировать не только электрические принципиальные схемы, но и функциональные схемы динамических систем с обратными связями, а также решать системы дифференциальных уравнений.
Рассмотрим в качестве примера усилитель постоянного тока с квадратором в цепи обратной связи, функциональная схема которого показана на рис. 3.11, а. При бесконечно большом коэффициенте передачи усилителя


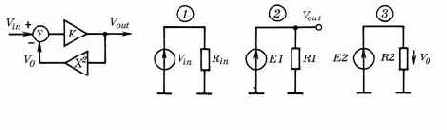 а - устройство вычисления квадратного корня; б - эквивалентная принципиальная схема для PSpice |
Составим схему замещения этого усилителя, используя компоненты, разрешенные в программе PSpice (рис. 3.11, б). С помощью нелинейного источника E1 осуществляется вычитание напряжений


Rin 1 0 1MEG
E1 2 0 POLY(2) (1,0) (3,0) 0 1E6 -1E6; усилитель-сумматор
R1 2 0 1MEG
E2 3 0 POLY(2) (2,0) (2,0) 0 0 0 0 1; квадратор
R2 3 0 1MEG
Замечание. Отметим, что с появлением в схемном редакторе Schematics библиотеки символов функциональных блоков amb.slb можно не составлять электрические схемы замещения функциональных схем типа рис. 3.11, б, а сразу составлять функциональные схемы из имеющихся стандартных блоков (см. Приложение 1).
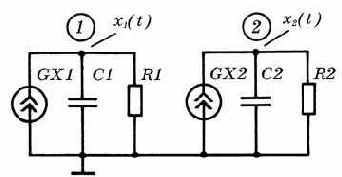
Продемонстрируем методику решения дифференциальных уравнений
на примере следующей системы уравнений:

с начальными условиями


DIFFERENTIAL EQUATIONS
GX1 0 1 POLY(3) (1,0) (2,0) (0,0) 0 -0.3 1 0 1 -3 0 0 0 0 1
GX2 0 2 POLY(3) (1,0) (2,0) (0,0) 0.6 0 -0.6 0 0 4 0 0 0 0 0 -6
C1 1 0 1
C2 2 0 1
R1 1 0 1E9
R2 2 0 1E9
.IC V(1)=0 V(2)=0.4
.TRAN 0.1s 40s SKIPBP
 |

3.2.5. Аналоговые функциональные блоки
Аналоговые функциональные блоки моделируются с помощью источников напряжения (E) или тока (G). В отличие от рассмотренных выше зависимых источников здесь разрешается использовать параметры и любые функции от узловых потенциалов, токов (через независимые источники напряжения) и времени.
Нелинейные передаточные функции
задаются по формату
Exxx <+узел> <–узел> VALUE={<выражение>}
Gxxx <+узел> <–узел> VALUE={<выражение>}
После ключевого слова VALUE в фигурных скобках приводится алгебраическое выражение, зависящее от узловых потенциалов, разности узловых потенциалов, токов через независимые источники напряжения и времени, например
ESIGNAL 2 0 VALUE={50mV*SIN(6.28*100kHz*TIME)*V(3,4)}
GPW 6 0 VALUE={V(5)*I(VP)}
Здесь для текущего времени выделено ключевое слово TIME.
Область управляемых источников с нелинейным законом управления очень обширна. В частности, нелинейные проводимости или резисторы имитируются в программе PSpice с помощью источников напряжения, управляемых собственным током, или источников тока, управляемых собственным напряжением. Пример имитации нелинейного резистора дан на рис. 3.13; его описание имеет вид
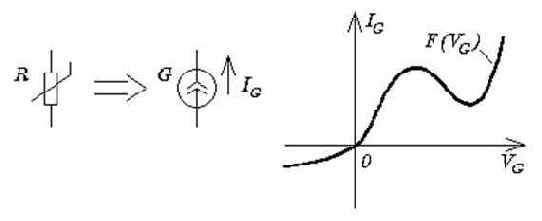 |
Нелинейная функция F(VG), описывающая нелинейную зависимость тока от падения напряжения на резисторе, должна быть определена в задании на моделирование до строки с описанием источника G, например
.FUNC F(X) = 1e-6*(1-EXP(-40*X))
Замечание. В режимах .TRAN и .DC значения источников Exxx, Ixxx вычисляются согласно приведенным в фигурных скобках выражениям. Если это выражение представляет собой линейную функцию нескольких переменных, то в режиме .AC данный источник представляет собой линейный управляемый источник.
При этом, если в выражение входит переменная TIME, она полагается равной нулю. Если же это выражение представляет собой нелинейную функцию одной переменной, то после расчета режима цепи по постоянному току выражение в фигурных скобках линеаризуется и в частотной области такой источник представляет собой линеаризированный управляемый источник. Нелинейную функцию нескольких переменных при расчете частотных характеристик использовать нельзя – результаты будут непредсказуемы. Эти же замечания справедливы и для описываемого ниже табличного задания управляемых источников.
Табличное описание
передаточной функции вводится по формату
Exxx <+узел> <–узел> TABLE {<выражение>} <<аргумент> <функция>>*
Gxxx <+узел> <–узел> TABLE {<выражение>} <<аргумент> <функция>>*
Входом таблицы является <выражение>, которое содержит любую комбинацию напряжений и токов. При обращении к управляемому источнику вычисляется значение выражения и берется значение функции из таблицы с помощью линейной интерполяции между опорными точками, задаваемыми парами чисел (<аргумент>,<функция>). Например, ВАХ туннельного диода, рассматриваемого как нелинейная проводимость (рис. 3.13), может быть задана в виде
GR 1 2 TABLE {V(GR)}=(0,0) (.01,1mA) (.02,1.1mA) (0.05,2mA)
+ (.06,3mA) (.065,3.2mA) (.8,1.5mA) (1,3mA) (1.5,5mA)
Координаты опорных точек задаются в порядке возрастания аргумента.
Заметим, что отсутствие аппроксимации табличных значений сплайнами более высоких порядков, чем линейная интерполяция, в ряде случаев приводит к слишком большим ошибкам.
Линейные функциональные блоки
моделируются в терминах соотношения между выходными и входными переменными в частотной области. По директиве .AC определяются значения комплексного коэффициента передачи блока на каждой частоте. При расчете рабочей точки по постоянному току и по директиве .DC берется значение коэффициента передачи на нулевой частоте (поэтому изображения по Лапласу всех узловых потенциалов не должны иметь составляющих типа 1/s).
По директиве . TRAN выходная переменная блока вычисляется как интеграл Дюамеля (свертка входного воздействия с импульсной характеристикой блока), что значительно увеличивает длительность расчетов. Возможны следующие варианты задания линейных блоков.
Передаточная функция управляемого источника задается с помощью преобразования Лапласа:
Exxx <+узел> <–узел> LAPLACE {<выражение>}=
+ {<передаточная функция в s-области>}
Gxxx <+узел> <–узел> LAPLACE {<выражение>}=
+ {<передаточная функция в s-области>}
Например, передаточная функция активного RC-фильтра задается следующим образом:
EARC 2 0 LAPLACE {V(9)}={5/(1+0.01*s)}
Фильтр с чебышевской передаточной функцией
задается в виде
Exxx <+узел> <–узел> CHEBYSHEV {<выражение>}= <тип>
+ <граничная частота>* <затухание>*
Gxxx <+узел> <–узел> CHEBYSHEV {<выражение>}= <тип>
+ <граничная частота>* <затухание>*
Здесь <тип> – тип фильтра, принимающий значение LP – фильтр нижних частот, HP – фильтр верхних частот, BP – полосовой фильтр, BR – режекторный фильтр. Для задания желаемой характеристики фильтра задается список граничных частот (для ФНЧ и ФВЧ задаются две частоты, для ПФ и РФ – четыре) и затем список затуханий на этих частотах в децибелах; порядок следования граничных частот безразличен. Приведем примеры:
E1 3 4 CHEBYSHEV {V(10)}=LP 800 1.2K 0.1dB 50dB
E2 5 6 CHEBYSHEV {V(10)}=BP 800 1.2K 2K 3K 0.1dB 50dB
Табличное описание
комплексной передаточной функции в частотной области задается по формату
Exxx <+узел> <–узел> FREQ {<выражение>}=[KEYWORD]
+ <<частота>,<модуль>,<фаза>>* [DELAY]=<задержка>]
Gxxx <+узел> <–узел> FREQ {<выражение>}=[KEYWORD]
+ <<частота>,<модуль>,<фаза>>* [DELAY]=<задержка>]
Здесь частота задается в герцах, модуль передаточной функции – в децибелах, фаза передаточной функции – в градусах. Значения опорных точек указываются в порядке возрастания частоты. Максимальное количество точек – 2048. Например, передаточная функция типа фильтра верхних частот задается следующим образом:
EHIGHPASS 2 0 FREQ {V(9)} (0,-60,69.1) (2kHz,-3,45) (5kHz,0,0)
С помощью ключевого слова KEYWORD изменяется способ задания таблицы передаточной функции. Оно может принимать следующие значения:
MAG – задание абсолютных значений передаточной функции вместо децибел;
DB – задание значений передаточной функции в децибелах (принимается по умолчанию);
RAD – задание фазы в радианах;
DEG – задание фазы в градусах (принимается по умолчанию);
R_I – задание действительной и мнимой части передаточной функции вместо ее модуля и фазы.
Ключевое слово DELAY задает дополнительную задержку, которая принимается во внимание при расчете фазовой характеристики фильтра.
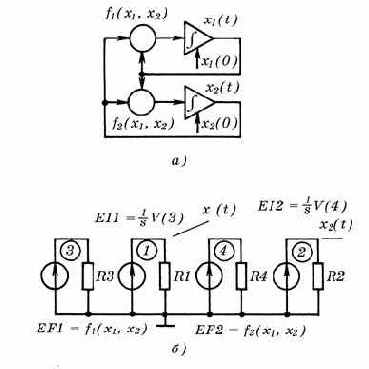
В качестве еще одного примера составим структурную схему моделирования рассмотренной выше системы дифференциальных уравнений

с помощью интеграторов [84]. На рис. 3.14, а
представлена функциональная схема моделирования этой системы уравнений, а на рис. 3.14, б – ее реализация в компонентном базисе программы PSpice. В ней использованы управляющие источники напряжения EI1, EI2, заданные с помощью преобразования Лапласа и выполняющие операции интегрирования, а также нелинейные управляемые источники напряжения EF1, EF2 для вычисления правых частей системы уравнений. На входном языке программы PSpice задание на решение рассматриваемой системы уравнений имеет вид
Laplace transforms
EI1 1 0 LAPLACE {V(3)}={1/s}
EI2 2 0 LAPLACE {V(4)}={1/s}
EF1 3 0 POLY(3) (1,0) (2,0) (0,0) 0 -0.3 1 0 1 -3 0 0 0 0 1
EF2 4 0 POLY(3) (1,0) (2,0) (0,0) 0.6 0 -0.6 0 0 4 0 0 0 0 0 -6
R1 1 0 1E9
R2 2 0 1E9
R3 3 0 1E9
R4 4 0 1E9
.IC V(1)=0 V(2)=0.4
.TRAN 0.1s 40s SKIPBP
 |
Полупроводниковые приборы, математические модели которых встроены в программу PSpice, описываются большим количеством параметров, задаваемых с помощью директивы .MODEL. Перечень и смысл этих параметров подробно объясняется в гл. 4. Директиву .MODEL можно поместить в описание анализируемой схемы или в файл библиотеки, доступ к которому осуществляется с помощью директивы .LIB. Описание конкретного полупроводникового прибора содержит его имя, номера узлов подключения, имя модели и коэффициент кратности Area, с помощью которого имитируется параллельное включение нескольких одинаковых приборов.
Диод описывается предложением
Dxxx <узел анода> <узел катода> <имя модели>
+ [<коэффициент кратности Area>]
Модель диода задается в виде
.MODEL <имя модели> D [(параметры модели)]
Пример 1. Включим между узлами 1 и 2 диод D9, параметры которого вводятся с помощью директивы .MODEL
D1 1 2 D9B
.MODEL D9B D (IS=5UA RS=14 BV=2.81 IBV=5UA)
Пример 2. Включим между узлами 1 и 2 диод D104A, параметры которого записаны в библиотечном файле d.lib
D1 1 2 D104A
.LIB D.LIB
Биполярный транзистор
описывается предложением
Qxxx <узел коллектора> <узел базы> <узел эмиттера>
+ [<узел подложки>] <имя модели> [<коэффициент кратности Area>]
Модели биполярных транзисторов задаются в виде
.MODEL <имя модели> NPN [(параметры модели)]
.MODEL <имя модели> PNP [(параметры модели)]
.MODEL <имя модели> LPNP [(параметры модели)]
Полевой транзистор с управляющим p–n-переходом описывается предложением
Jxxx <узел стока> <узел затвора> <узел истока>
+ <имя модели> [<коэффициент кратности Area>]
Модели полевых транзисторов задаются в виде
.MODEL <имя модели> NJF [(параметры модели)]
.MODEL <имя модели> PJF [(параметры модели)]
Арсенид-галлиевый полевой транзистор
с управляющим p–n-переходом и каналом n-типа описывается предложением
Bxxx <узел стока> <узел затвора> <узел истока>
+ <имя модели> [<коэффициент кратности Area>]
Модель арсенид-галлиевого полевого транзистора задается в виде
.MODEL <имя модели> GASFET [(параметры модели)]
МОП-транзистор описывается предложением
Mxxx <узел стока> <узел затвора> <узел истока>
+ <узел подложки> <имя модели>
+ [L=<значение>] [W=<значение>] [AD=<значение>]
+ [AS=<значение>] [PD=<значение>] [PS=<значение>]
+ [NRD=<значение>] [NRS=<значение>] [NRG=<значение>]
+ [NRB=<значение>] [M=<значение>]
Необязательные параметры приведены в табл. 3.16.
Таблица 3.16
|
Обозначение |
Параметр |
Значение по умолчанию |
Размерность |
|
L |
Длина канала |
DEFL |
м |
|
W |
Ширина канала |
DEFW |
м |
|
AD |
Площадь диффузионной области стока |
DEFAD |
м |
|
AS |
Площадь диффузионной области истока |
DEFAS |
м |
|
PD |
Периметр диффузионной области стока |
0 |
м |
|
PS |
Периметр диффузионной области истока |
0 |
м |
|
NRD |
Удельное относительное сопротивление стока |
1 |
|
|
NRS |
Удельное относительное сопротивление истока |
1 |
|
|
NRG |
Удельное относительное сопротивление затвора |
0 |
|
|
NRB |
Удельное относительное сопротивление подложки |
0 |
|
|
M |
Масштабный коэффициент |
1 |
Параметры L и W могут быть заданы при описании модели МОП-транзистора по директиве .MODEL; кроме того, параметры L, W, AD и AS по умолчанию принимают значения, присваиваемые по директиве .OPTIONS (см. разд. 3.3.7).
Модели МОП-транзисторов задаются в виде
.MODEL <имя модели> NMOS [(параметры модели)]
.MODEL <имя модели > PMOS [(параметры модели)]
3.2.7. Макромодели
Отдельные фрагменты цепи или схемы замещения компонентов имеет смысл оформлять в виде макромоделей (подсхем). Описание макромодели начинается директивой .SUBCKT и заканчивается директивой .ENDS. Между ними помещаются описания компонентов, входящих в состав макромодели
.SUBCKT <имя макромодели> <список узлов>
+ [OPTIONAL:<<узел интерфейса>=<значение по умолчанию>>*]
+ [PARAMS:<имя параметра>=<значение>*]
+ [TEXT:<<имя текстовой переменной>=< текст>>*]
{описание компонентов}
.ENDS [имя макромодели]
Ключевое слово OPTIONAL используется для спецификации одного или более необязательных узлов макромодели – указываются имя узла и его значение по умолчанию. Если при вызове макромодели эти узлы не указываются, используются их значения по умолчанию, что удобно для задания источников питания цифровых устройств. После ключевого слова PARAMS приводится список параметров, значения которых передаются из основной цепи в макромодель, после ключевого слова TEXT – текстовая переменная, передаваемая из описания основной цепи в описание макромодели (используется только при моделировании цифровых устройств).
Между директивами .SUBCKT и .ENDS можно помещать описания других макромоделей и другие директивы (начиная с версии Design Center 5.4). Приведем пример:
* Макромодель операционного усилителя K140УД6A
* Создана с помощью программы Parts
* Соединения: неинвертирующий вход
* ¦ инвертирующий вход
* ¦ ¦ источник положительного питания
* ¦ ¦ ¦ источник отрицательного питания
* ¦ ¦ ¦ ¦ выход
* ¦ ¦ ¦ ¦ ¦
.subckt K140UD6A 1 2 3 4 5
c1 11 12 2.887E-12
c2 6 7 30.00E-12; емкость внутренней коррекции
dc 5 53 dx
de 54 5 dx
dlp 90 91 dx
dln 92 90 dx
dp 4 3 dx
egnd 99 0 poly(2) (3,0) (4,0) 0 .5 .5
fb 7 99 poly(5) vb vc ve vlp vln 0 12.38E6 -10E6 10E6 10E6 -10E6
ga 6 0 11 12 188.5E-6
gcm 0 6 10 99 18.85E-9
iee 10 4 dc 75.06E-6
hlim 90 0 vlim 1K
q1 11 2 13 qx
q2 12 1 14 qx
r2 6 9 100.0E3
rc1 3 11 5.305E3
rc2 3 12 5.305E3
re1 13 10 4.612E3
re2 14 10 4.612E3
ree 10 99 2.665E6
ro1 8 5 30
ro2 7 99 30
rp 3 4 11.01E3
vb 9 0 dc 0
vc 3 53 dc 3
ve 54 4 dc 3
vlim 7 8 dc 0
vlp 91 0 dc 25
vln 0 92 dc 25
.model dx D ( Is=800.0E-18 )
.model qx NPN ( Is=800.0E-18 Bf=1.250E3 )
.ends
Вызов макромодели, т. е. включение ее в нужное место цепи, осуществляется предложением
Xxxx <список узлов> <имя макромодели>
+ [PARAMS:<<имя параметра>=<значение>>*]
+ [TEXT:<<имя текста>=<текст>>*]
Например, описанная выше макромодель ОУ К140УД6А может быть включена в схему предложением
X1 4 0 15 16 8 K140UD6A
Имена узлов, устройств и моделей в описании макромодели являются локальными. Поэтому в основной цепи и в макромодели можно использовать совпадающие имена. При обращении в основной цепи к какому-нибудь имени макромодели применяют так называемые составные имена. Они образуются из имени макромодели и внутреннего имени, разделенных точкой. Например, конденсатор C2 макромодели X1 имеет составное имя X1.C2. При ссылке на компоненты макромоделей составные имена заключаются в квадратные скобки, например, V([XOP1.X3.R2]) – падение напряжения на резисторе R2, который входит в состав макромодели X3, которая, в свою очередь, является составной частью макромодели операционного усилителя XOP1.
В программе PSpice имеются встроенные макромодели операционного усилителя, компаратора напряжения, регулятора напряжения и
стабилизатора напряжения, параметры которых рассчитываются специальной программой Parts по их паспортным данным (разд. 7.3). Кроме того, имеются макромодели оптоэлектронных приборов, тиристоров, кварцевых резонаторов и т. п., составляемые фирмами-производителями и отдельными пользователями (см. гл. 5).
Заметим, что использование встроенной модели ОУ при расчете схем, состоящих даже из небольшого количества ОУ, приводит к большим затратам машинного времени. Поэтому в тех случаях, когда не требуется высокая точность воспроизведения динамических характеристик ОУ, целесообразно применять упрощенные модели ОУ, примеры которых приведены в [14].
Описание макромодели можно поместить непосредственно в файл задания на моделирование или в библиотечный файл макромоделей ОУ, например с именем op.lib. Тогда для включения этого ОУ в схему необходимо сначала по директиве .LIB обеспечить доступ к этому файлу и затем указать номера узлов подключения макромодели
.LIB D:\PSPICE\LIB\op.lib
X1 17 18 0 22 9 25 K140UD8A
Обратим внимание на механизм передачи параметров из описания основной схемы в описание макромодели и проиллюстрируем его на следующем примере. Рассмотрим фрагмент описания схемы
Test
.param C=1p LK=8m
.step param C list 5p 10p
X1 5 20 DL params: C={C} L={LK}
.subckt DL 1 2 params: C=0 LK=5m R=1k
R1 1 2 {R}
C1 2 0 {C}
L1 1 2 {LK}
.ends DL
. . . . . . . .
.end
Здесь в директиве .subckt определены параметры макромодели C и R и заданы их значения по умолчанию. При вызове макромодели X1 указаны значения параметра C, принимающего значения 5 и 10 пФ, и параметра LK=8 мГн. Сопротивление резистора R1 по умолчанию принимает значение 1 кОм. Здесь специально подчеркнуто, что локальные и глобальные параметры могут принимать как совпадающие (C={C}), так и различные (L={LR}) обозначения.
