Магнитный сердечник
В программе PSpice используется модель магнитного сердечника, предложенная Джилсом и Атертоном [52]. Она основана на известных представлениях о движении доменных границ магнитных материалов. С ее помощью удается отразить все основные характеристики гистерезиса, такие, как кривая начальной намагниченности, намагниченность насыщения, коэрцитивная сила, остаточная намагниченность и динамические потери на гистерезис.
Существуют две разновидности этой модели – LEVEL=1 и LEVEL=2. Их параметры приведены в табл. 4.9.
Таблица 4.9
| Имя параметра | Параметр | Размерность | Значение по умолчанию | ||||
| LEVEL | Индекс модели | 2 | |||||
| AREA | Площадь поперечного сечения магнитопровода | см | 0,1 | ||||
| PATH | Средняя длина магнитной силовой линии | см | 1 | ||||
| GAP | Ширина воздушного зазора | см | 0 | ||||
| PACK | Коэффициент заполнения сердечника | 1 | |||||
| MS | Намагниченность насыщения | А/м | 500·10 | ||||
| A | Параметр формы безгисте- резисной кривой намагничивания | А/м | 10 | ||||
| C | Постоянная упругого смещения доменных границ | 0,1 | |||||
| K | Постоянная подвижности доменов | А/м | 10 | ||||
| ALPHA | Параметр магнитной сваязи доменов | 10 | |||||
| GAMMA | Параметр демпфирования доменов (для LEVEL=1) | 1/с | 0 |
Параметры AREA, PATH, GAP и PACK определяются геометрическими размерами сердечника, остальные – свойствами магнитного материала. Основная особенность модели LEVEL=1 – учет частотных свойств магнитных материалов. Модель LEVEL=2 обеспечивает достаточную точность для ферритовых сердечников и сердечников из молибденовых пермаллоев, а также может быть использована для моделирования ферромагнетиков аморфной структуры. В последующих версиях PSpice модель LEVEL=1 использоваться не будет, так как модель LEVEL=2 усовершенствована и обеспечивает большую точность моделирования. Поэтому программа Parts в системе Design Center 6.2 создает модели LEVEL=2. При использовании моделей из старых версий, в кторых по умолчанию назначался параметр LEVEL=1, в версии Design Center 6.2 его нужно явно указать в директиве .MODEL.
Краткое описание модели магнитного сердечника. Магнитный материал, состоящий из множества доменов, находящихся в равновесном состоянии, имеет идеальную (безгистерезисную) кривую намагничивания. Безгистерезисная кривая получается в том случае, когда в дополнение к постоянной составляющей на магнитный материал воздействует сильное переменное поле с амплитудой, постепенно убывающей до нуля. Эта кривая соответствует минимальной энергии доменов и моделируется уравнением
Man(Hэф)= MS·F(Hэф/A), (1)
где
Hэф = H + ALPHA·Man,

Man – безгистерезисная намагниченность, MS – намагниченность насыщения, Hэф – эффективная напряженность поля, для модели LEVEL=2 полагают ALPHA=0.
Заметим, что кривая начальной намагниченности магнитных материалов всегда лежит ниже безгистерезисной кривой, как показано на рис. 4.12; в области насыщения они сливаются. Безгистерезисная кривая представляет собой как бы "хребет" кривой гистерезиса.
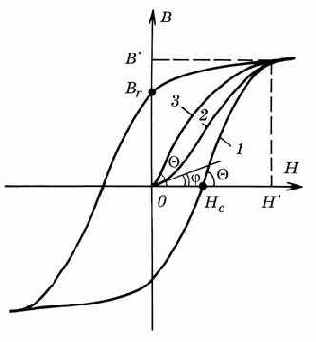 Рис. 4.12. Петля гистерезиса (1), начальная (2) и безгистерезисная (3) кривые намагничивания |
безгистерезисная намагниченность Man
соответствует такому состоянию, который материал мог бы достичь, если домены могли свободно перемещаться. Однако реально домены такой свободой не обладают из-за наличия потенциальных барьеров в промежуточных переходных состояниях. Границы доменов остаются неподвижными до тех пор, пока не накопится достаточный магнитный потенциал для скачкообразного изменения положения границ (скачки Баркгаузена). Для этого требуется некоторая удельная энергия на единицу объема материала, что аналогично эффекту "сухого трения". Уравнение магнитного материала в этом случае имеет вид

где M – намагниченность материала;

при dH/dt>0, и

Это справедливо при необратимом движении доменов. Величина Man рассчитывается из выражения (1). При перемагничивании проявляются эффекты упругого смещения границ доменов, так что намагниченность уже не может описываться уравнением (2). В предположении сферического прогиба доменной границы теоретическая зависимость дифференциальной магнитной проницаемости ферромагнетика принимает вид

Решение системы уравнений (1), (3) позволяет рассчитать кривую гистерезиса магнитного сердечника без воздушного зазора.
Влияние воздушного зазора. Если ширина воздушного зазора мала по сравнению с другими размерами сердечника, можно предположить, что все силовые линии магнитного поля пересекают зазор без изменения направления и что краевые эффекты малы. В таком случае справедливо соотношение
H·L + Hз·Lз = nI, (4)
где H – напряженность поля в сердечнике; L=PATH – средняя длина магнитопровода; Hз – напряженность поля в зазоре; Lз=GAP – длина зазора; nI –произведение числа витков катушки сердечника на протекающий по ним ток. Предположим, что намагниченность в воздушном зазоре пренебрежимо мала, так что Bз=Hз (т.е. магнитная проницаемость

H·L + Bз·Lз = nI.
Предлагается графический метод решения составленной системы уравнений, который заключается в следующем:
1) с помощью уравнений (1), (3) рассчитывается кривая B–H без учета зазора;
2) для построения кривой B–H с учетом зазора для каждого текущего значения H проводится линия с наклоном -L/Lз (при Lз=0 вертикальная прямая);
3) находится точка пересечения этой линии с кривой B–H, построенной без учета зазора (точка a на рис. 4.13). Ордината точки пересечения определяет магнитную индукцию сердечника B с учетом наличия зазора (точка a' на рис. 4.13).
Этот метод численно реализован в программе PSpice.
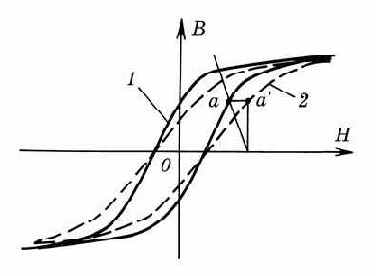 Рис. 4.13. Петля гистерезиса без учета (1) и с учетом (2) воздушного зазора |
определяются из дифференциального уравнения:

Напомним, что ЭДС самоиндукции E=-dФ/dt= –S·dB/dt
, где S=AREA·PACK – эффективная площадь поперечного сечения магнитопровода. Напряженность поля H связана с током в катушке сердечника I соотношением H=nI/L. Поэтому в уравнении (5) производная dM(t)/dt
определяется приложенным к обмотке сердечника напряжением, намагниченность в статическом режиме M(H)
определяется из уравнений (1) – (3), в результате чего находится скорректированное значение намагниченности M(t)
с учетом частотнозависимых потерь.
Система единиц. В программе PSpice рассчитывается зависимость намагниченности M от H, а перед построением кривой гистерезиса B–H
с помощью программы Probe производится расчет магнитной индукции B=

в А/м, магнитная индукция B в гауссах, напряженность магнитного поля H
в эрстедах [ 1 Э =


Определение параметров модели магнитного сердечника по экспериментальным данным. Расчет параметров модели магнитного сердечника LEVEL=2 по экспериментальным данным возможна с помощью программы Parts (разд. 7.3). Приведем здесь методику ручной настройки модели сердечника по экспериментальным данным с помощью программ PSpice и Probe. Настройка производится в несколько этапов.
1. Сначала подбирают параметры A и ALPHA модели, обеспечивая совпадение теоретических (т.е. рассчитанных с помощью программы PSpice) и экспериментальных безгистерезисных кривых намагничивания. Безгистерезисные кривые обычно не приводятся в справочных данных, поэтому их необходимо экспериментально измерить [12].
Угол наклона безгистерезисной кривой при H=0 примерно равен углу наклона кривой гистерезиса B–H в точке пересечения с осью абсцисс. Из уравнения (1) следует, что угол наклона кривой гистерезиса при H=Hc равен (рис. 4.12)
tg

Намагниченность насыщения MS определяется на основе магнитной индукции B' на участке насыщения (рис. 4.12):
MS = B'/0,01257 – H',
где H' – напряженность поля, при котором измерена индукция B'.
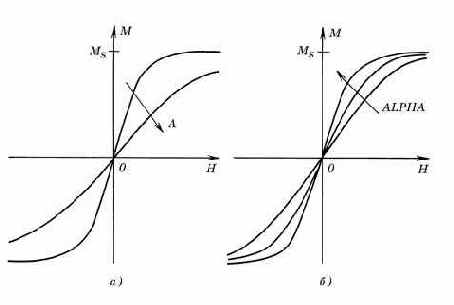 Рис. 4.14. Зависимость формы безгистерезисной кривой (К=0) от параметров А (а) и ALPHA (б) |

2. Далее экспериментально измеряют или берут из справочных данных начальную кривую намагничивания и петлю гистерезиса и повторяют моделирование при K и C, не равных нулю.
Сначала подбором константы C получают требуемое значение начальной магнитной проницаемости

При этом учитывают, что параметр С равен отношению магнитных проницаемостей



Рис. 4.15. Зависимость начальной кривой намагничивания от параметра K |
Значение K влияет на ширину петли гистерезиса. При подборе K следует обеспечить правильное значение коэрцитивной силы Hc (рис. 4.12).
Для точной подгонки экспериментальных и теоретических кривых гистерезиса, в частности, для обеспечения заданного значения остаточной магнитной индукции Br, следует снова слегка проварьировать параметры A и ALPHA. В отсутствии экспериментальных безгистерезисных кривых подбор параметров модели магнитного сердечника производится в той же последовательности, но занимает большее время.
3. Учет зависимости потерь в магнитном материале от частоты предусматривается в модели LEVEL=1. Для идентификации параметра GAMMA полагают сначала ее равной верхней граничной частоте материала и моделируют кривую гистерезиса при заданной частоте сигнала. Затем подбором GAMMA добиваются совпадения ширины кривой B–H экспериментальным данным. При этом имеют в виду, что увеличение GAMMA уменьшает потери в сердечнике.
Оригинальная методика идентификации параметров моделей ферромагнетиков по экспериментальным данным приведена в статье [11]. В частности, в ней приведены параметры модели аморфного магнитного материала 84КХСР, используемого для изготовления витых магнитопроводов высокочастотных импульсных трансформаторов источников вторичного электропитания
MS=500·10

Пример. Приведем для иллюстрации пример задания на моделирование сердечника Б14 на феррите M2000-НМ1 с помощью PSpice. Начальная кривая намагничивания и петля гистерезиса рассчитывается с помощью следующего задания:
Demonstration of inductor B-H curve
I1 0 1 SIN ( 0 0.2 250 0 0 0)
L1 1 0 20
K1 L1 0.9999 M2000
R1 1 0 500
.model M2000 CORE (LEVEL=1 MS=334e3 ALPHA=2.3e-2
+ A=4050 K=166 C=0.05 AREA=0.064 PATH=2.25)
.tran 1u 5m SKIPBP
.probe
.END
После завершения моделирования с помощью программы PSpice вызывают графический постпроцессор Probe, по оси X откладывают переменную в эрстедах, выполняя последовательность команд Plot/X Axis Settings/Axis Variable (для выбора имени переменной H(K1) из списка доступных переменных нужно включить опцию Internal Subcircuit Nodes). По оси Y выводят график функции B(K1) в гауссах (см.п. 3.2.1 и разд. 7.2), выполняя команду Trace/Add.
